This year in the Competition Division, we will conduct a type of a territory game to compete over which team can take more squares on a field divided up into grids. The students will become players and decide on the movements of agents that move about on the game field. The battle proceeds with the 2 teams taking turns, and in each turn, the agents from the both team will move simultaneously. The players have to send to the server all the agents’ movements within the specified time. The team with greater total points calculated from the agent occupying after a set number of turns are conducted, wins the match. The result of the match is determined from the total point gained in these 2 games. For the disclosed field, you will need to strategically analyze the field in advance, while for the non-disclosed field you will need a flexible strategy. The key to winning the game will be to construct a system that can adapt to either type strategies. Let the agents move about freely on the field as they are dancing around. Competition Field 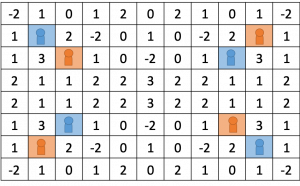

- The field provided is maximum of 20 squares × 20 squares and minimum of 10 squares × 10 squares. The size of the field varies among the battles. The shape of the field is always a rectangle.
- The number of agents varies according to the field used. Number of agents per team is maximum of 8 and minimum of 2.
- Team A agent ( )and Team B agent ( ) are positioned on one of the squares. The agent will not necessarily be positioned in the outer squares but may be positioned towards the center of the field.
- On the square that the agent is first positioned, the agent’s team’s tile will be positioned.
- Points in whole numbers equal to or greater than -16 and equal to or less than 16 will be given to all the squares. However, the total of poitns all squares will not be less than 0. The agent may be first positioned on square with point less than 0.
- For fairness in the first setting, the agents and the field are positioned symmetrically.